Limites Laterales

En la definición de límite de una función en un punto decíamos que era el valor al que se aproximaba la función f(x) cuando la x se acercaba a a. Pero a a, siempre que sea un valor finito, podemos acercarnos por la izquierda, esto es, tomando valores menores que a, o por la derecha, es decir, tomando valores mayores que a. Los límites laterales contamplan precisamente estas dos posibilidades.

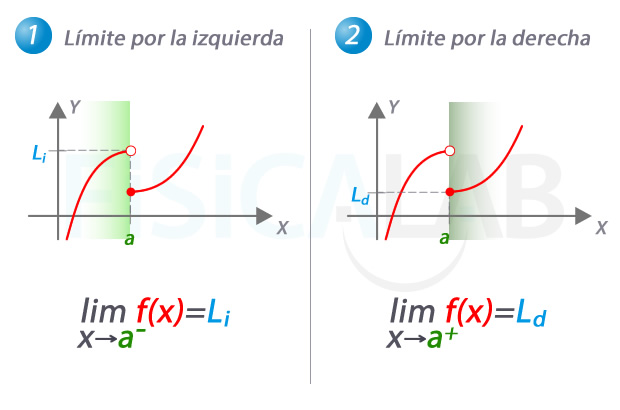
A la izquierda, en 1, concepto y notación del límite por la izquierda. Observa que, a medida que tomamos valores próximos a a, pero menores que este (fondo verde claro), los correspondientes valores de f(x), en rojo, se aproximan a Li. Decimos que Li es el valor del límite de la función cuando x se aproxima a a por la izquierda.

En 2, el concepto y notación del límite por la derecha. A medida que tomamos valores próximos a a, pero mayores que este (fondo verde oscuro), los correspondientes valores de f(x) se aproximan a Ld. Decimos que Ld es el valor del límite de la función cuando x se aproxima a a por la derecha.

Limites por izquierda

El valor del límite de una función f(x) cuando x tiende a a por la izquierda es el valor al que se acerca y=f(x) cuando x se acerca a a tomando valores menores que a. Pueden darse los siguientes casos.

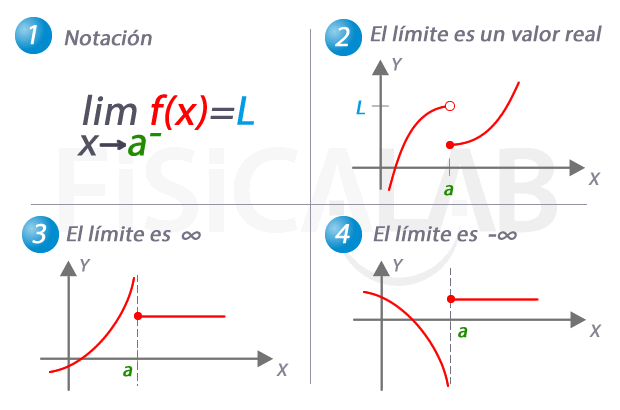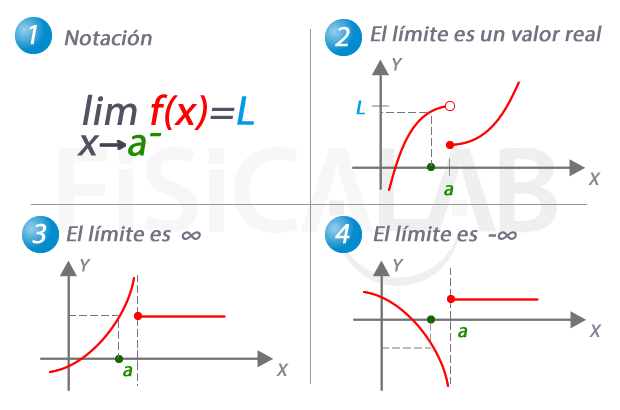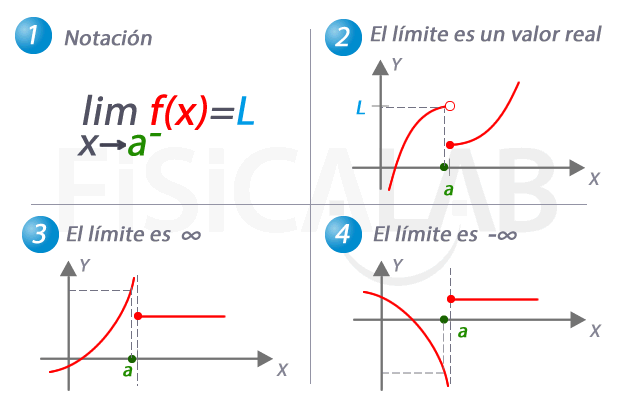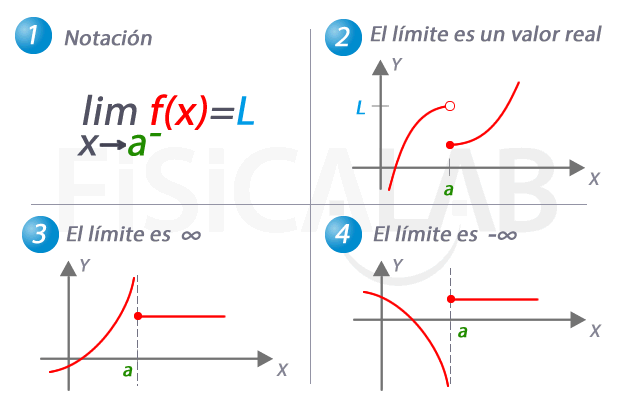
En 1 te presentamos la notación utilizada para referirnos al límite por la izquierda de una función. En 2, 3 y 4 tenemos tres casos concretos que pueden darse. En 2 el límite por la izquierda es una valor real concreto, L. Observa como el valor del límite no tiene porqué coincidir con el de la función en el punto. En 3, el límite por la izquierda es infinito, y por tanto, a medida que nos aproximamos a a la función crece indefinidamente. En 4, el caso complementario, el límite por la izquierda es menos infinito.

Daremos una definición formal distinguiendo cada uno de esos casos:

Limite Infinito

Decimos que el límite de una función cuando x se aproxima a a por la izquierda es infinito cuando para cualquier valor k (en el eje y), tan grande como se quiera, siempre se puede encontrar un valor real positivo δ (en el eje x) tal que las imágenes de cualquier x comprendido entre a-δ y a serán siempre mayores que k.

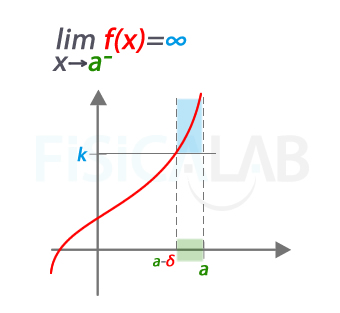
Decimos que limf(x)=∞ porque para cualquier valor k en el eje y, podemos encontrar un valor δ positivo a partir del cual los valores de las imágenes de cualquier x que se encuentre en el intervalo de fondo verde (intervalo a-δ<x<a) quedan por encima de k.

Limite Finito

Decimos que limxf(x)=L, siendo L un valor finito, cuando para cualquier entorno de L que tomemos, con radio ε, podemos encontrar un δ>0, tal que las imágenes de x que se encuentran en el intervalo a-δ<x<a están dentro del entorno de L, es decir, |f(x)-L|<ε.

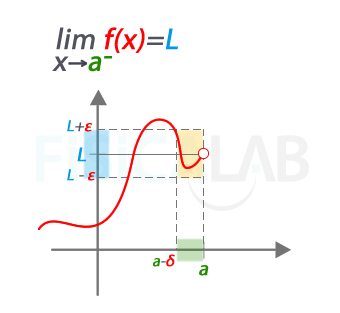
Decimos que limxf(x)=L porque para cualquier valor ε, por pequeño que sea, podemos encontrar un valor δ positivo a partir del cual los valores de las imágenes de cualquier x que se encuentre en el intervalo de fondo verde (intervalo a-δ<x<a) quedan en el interior del entorno de L de radio ε (intervalo de fondo azul).

Limite por Derecha

El valor del límite de una función f(x) cuando x tiende a a por la derecha es el valor al que se acerca y=f(x) cuando x se acerca a a tomando valores mayores que a. Pueden darse los siguientes casos.

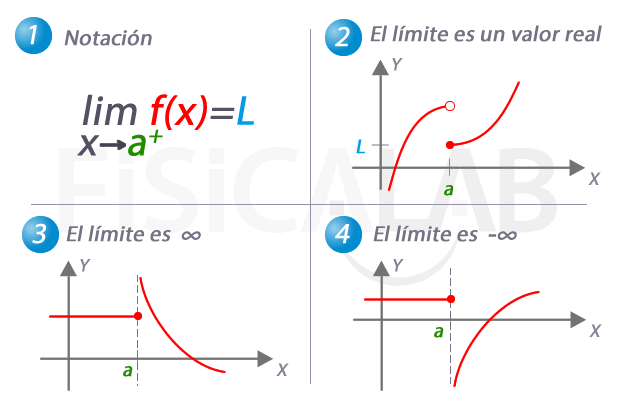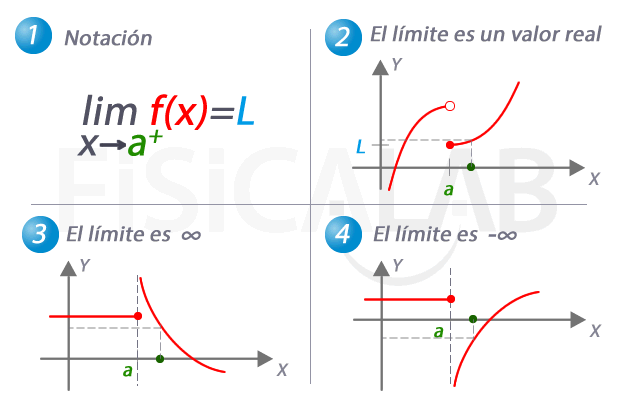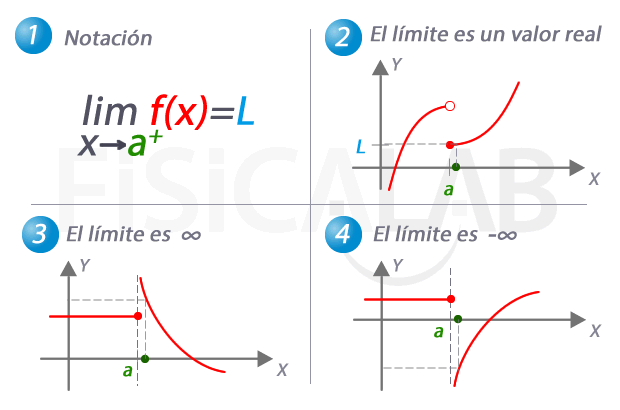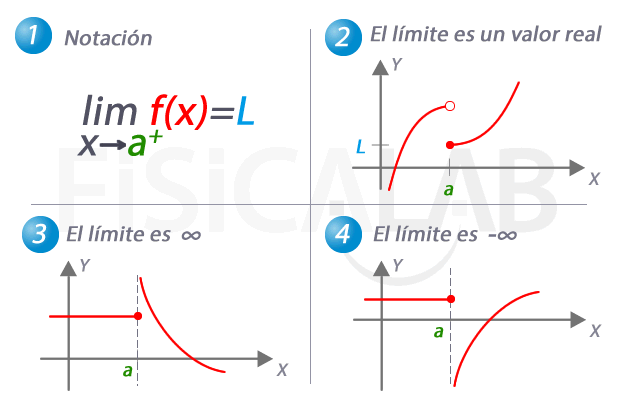
En 1 te presentamos la notación utilizada para referirnos al límite por la derecha de una función. En 2, 3 y 4 tenemos tres casos concretos que pueden darse. En 2 el límite por la derecha es una valor real concreto, L. En 3, el límite por la derecha es infinito, y por tanto, a medida que nos aproximamos a a la función crece indefinidamente. En 4, el caso complementario, el límite por la derecha es menos infinito.

Limite Infinito

Decimos que el límite de una función cuando x se aproxima a a por la derecha es infinito cuando para cualquier valor k (en el eje y), tan grande como se quiera, siempre se puede encontrar un valor real positivo δ (en el eje x) tal que las imágenes de cualquier x comprendido entre a y a+δ serán siempre mayores que k.

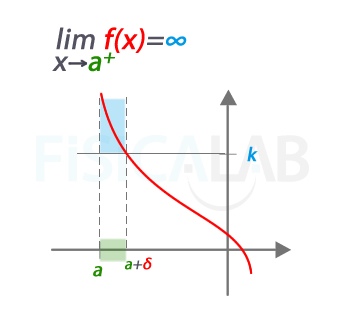
Decimos que limf(x)=∞ porque para cualquier valor k en el eje y, podemos encontrar un valor δ positivo a partir del cual los valores de las imágenes de cualquier x que se encuentre en el intervalo de fondo verde (intervalo a<x<a+δ) quedan por encima de k.

Limites menos infinito

Decimos que el límite de una función cuando x se aproxima a a por la derecha es menos infinito cuando para cualquier valor k (en el eje y), negativo y tan grande en valor absoluto como se quiera, siempre se puede encontrar un valor real positivo δ (en el eje x) tal que las imágenes de cualquier x comprendido entre a y a+δ serán siempre menores que k.

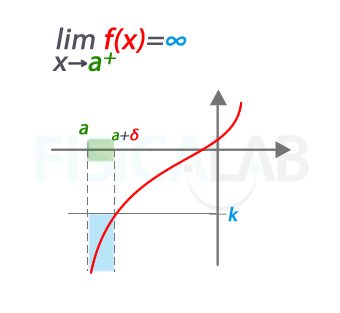
Decimos que limxf(x)=−∞ porque para cualquier valor k negativo en el eje y, podemos encontrar un valor δ positivo a partir del cual los valores de las imágenes de cualquier x que se encuentre en el intervalo de fondo verde (intervalo a<x<a+δ) quedan por debajo de k.

Limite Finito

Decimos que limxf(x)=L, siendo L un valor finito, cuando para cualquier entorno de L que tomemos, con radio ε, podemos encontrar un δ>0, tal que las imágenes de x que se encuentran en el intervalo a<x<a+δ están dentro del entorno de L, es decir, |f(x)-L|<ε.

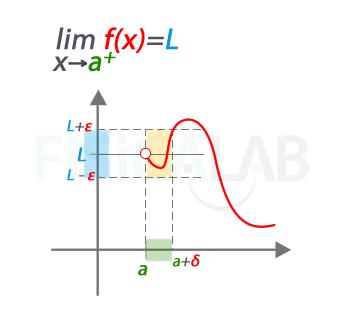
Decimos que limxf(x)=L porque para cualquier valor ε, por pequeño que sea, podemos encontrar un valor δ positivo a partir del cual los valores de las imágenes de cualquier x que se encuentre en el intervalo de fondo verde (intervalo a<x<a+δ) quedan en el interior del entorno de L de radio ε (intervalo de fondo azul).

Calculo

En general, para determinar el valor de los límites laterales se sigue el mismo procedimiento que ya hemos visto para el cálculo del límite de una función en un punto, pero con algunas consideraciones adicionales. Así, si f(x) es una función habitual definida por una sola expresión analítica y que está definida en el entorno de x=a, entonces el valor del límite de la función cuando x tiende a a- (o a a+) es f(a-)≃f(a) (o f(a+)≃f(a)). Por ejemplo:

Observa que tanto 3+, que significa un número un poquito más grande que 3, como 3-, que significa un número un poquito más pequeño que 3, son, en términos de límite, igual a 3. Atención especial merece el 0, en el que hay que tener en cuenta que 0- es negativo y 0+ es positivo. De ahí que (0-)2=0+.

Por otro lado, puede ocurrir también que:

• f(x) presente un denominador que se anula y un numerador que no se anula en x=a, es decir, una indeterminación del tipo k/0. En este caso, el límite será infinito o menos infinito, según sea la relación entre el signo del numerador y el del denominador. Es importante tener el cuenta el - o el + de a- o a+. Ejemplos:

• f(x) presente un cambio de rama en x=a. En este caso, tendremos que tomar, para el cálculo, la rama correspondiente al - o el + de a- o a+. Ejemplos: