Limite de una Funcion en un punto

 Limite de una Funcion

De manera intuitiva, el límite de una función real en un punto 'a' es el valor L al que se aproxima la función (es decir, su coordenada y) a medida que la coordenada x se aproxima a a. En la siguiente imagen queda recogido el concepto y la notación que se suele utilizar:

notación y concepto de límite de una función

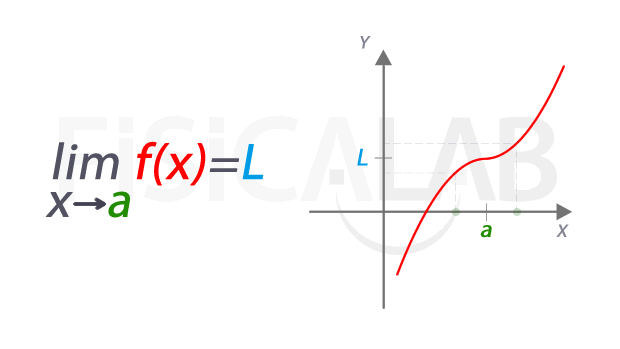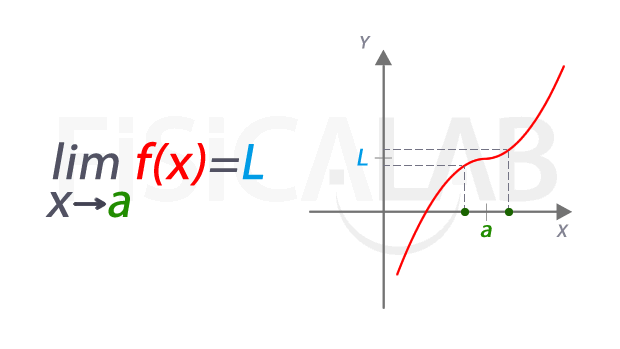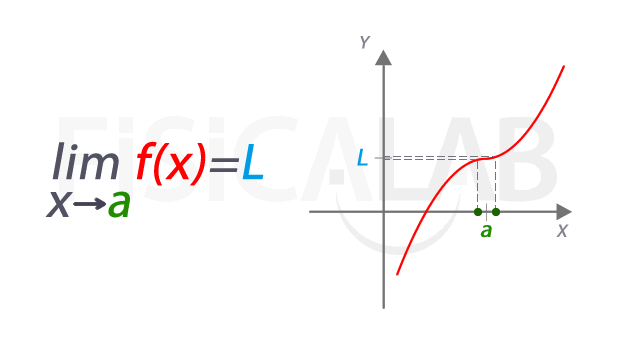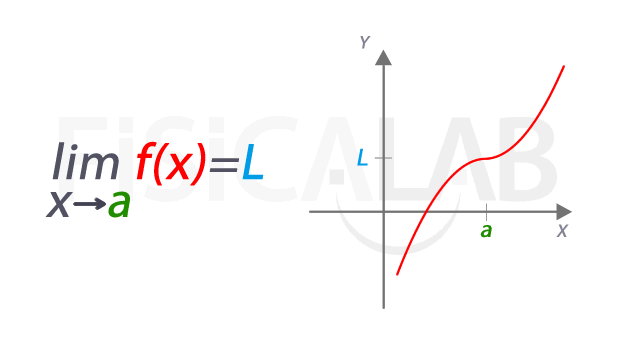
A la izquierda la notación empleada para referirnos al límite. Se lee "límite de f(x) cuando x tiende a a" . El valor del límite es L, representado en azul. La función f(x) está en rojo, y el punto en el que estamos estudiando el límite tiene una coordenada x cuyo valor es a, en verde. A la derecha esta misma idea representada de manera dinámica. A medida que nos acercamos a x=a, las correspondientes imágenes se aproximan al valor del límite L. Aunque en este caso, el valor del límite coincide con el de la función en el punto, pues f(a)=L, en realidad se trata de dos conceptos distintos, como veremos más abajo.

Aproximaciones Sucesivas

Imagina que te pedimos que recorras la mitad de la distancia que te separa de la puerta de tu habitación. Una vez allí, te pedimos que lo hagas de nuevo... y una vez allí, una vez más... ¿Llegarías finalmente a recorrer la distancia que te separaba de la puerta al principio si seguimos dándote, una y otra vez, la misma orden? 

Lo cierto es que en cada iteración te aproximarías al valor de la distancia total, y, si repitieras el proceso infinitas veces, efectivamente, lo alcanzarías. Apliquemos a una función esta idea de aproximarnos sucesivamente a un punto:





¿Qué valor alcanza la función (es decir, su coordenada y) cuando la x se aproxima a 3?

Tu primera tentación puede ser intentar calcular f(3)... pero vemos que queda 0/0, y ya sabemos que no tiene sentido en matemáticas dividir entre 0 (y mucho menos si el número que divido es el propio cero). Pero observa qué ocurre cuando hacemos varias aproximaciones sucesivas:
















Como vemos, la sucesión de valores también nos conduce a 1. Por tanto, podemos decir que 1 es el límite de f(x)=x2−4x+32x−6 cuando x se aproxima a 3, y escribir:





Ejemplo de límite de una función

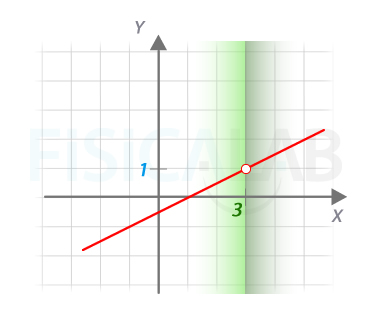
Observa que la función no está definida para x=3; sin embargo, tomando valores próximos, los valores de y correspondientes son cada vez más próximos a 1, ya sean los valores de x tomados por la izquierda (menores y representados un verde más claro) o por la derecha (mayores y representados en un verde más oscuro).


Aunque decimos "límite de una función en un punto", cuando calculamos el límite lo que hacemos es estudiar si las imágenes de la función se acercan a un valor concreto cuando la variable independiente x "tiende a" a (o "se acerca a" a). Dicho de otra manera, el límite es un concepto dinámico.


Comentarios

Publicar un comentario

Entradas más populares de este blog

Asintotas de una funcion

Imagen
 Una asíntota es una recta a la cual se aproxima indefinidamente una función, sin llegar nunca a tocarla. Tipos de asíntotas La palabra asíntota proviene del griego asumptotos que significa sin encontrarse. En la figura tenemos los 3 tipos de asíntotas que puede presentar una función: en verde, una asíntota horizontal; en rojo, una asíntota vertical; en azul, una asíntota oblicua. Como puedes ver, las ramas de la función nunca tocan a las asíntotas, pero se aproximan de manera constante a ellas. Como ves, gráficamente las asíntotas se asocian a ramas de la función infinitas (que no tienen fin). En este apartado aprenderemos a calcular: Asintotas Verticales Decimos que la recta x=k es una asíntota vertical de la función f(x) cuando se cumple: Donde: k: es el valor real del eje x al que se aproxima la función de forma indefinida, ya sea por la izquierda o por la derecha del mismo. Por ejemplo, -2,0 ó 1. Se dice que la función diverge en x=k f(x): Es la función que presenta la asíntot...
Leer más

Operaciones con Infinito

Imagen
 Operaciones con Infinito El infinito (∞) es un concepto que ha ocupado la mente de filósofos, matemáticos y grandes científicos a lo largo de la historia. Aunque la definición concreta depende del campo en el que nos encontremos (geometría, teoría de conjuntos, análisis de funciones), todas ellas tienen en común la noción de una cantidad sin límite. Para representar el infinito se utiliza un símbolo denominado lemniscata. En la figura puedes ver distintas representaciones del mismo. Corresponden todas al carácter Unicode U+221E (código ∞) en distintos tipos de letra. Su nombre proviene del griego λημνίσκος (lemniscos), que significa lazo. Aunque se asemeja bastante a un 8 tumbado, su forma precisa está descrita como el lugar geométrico de los puntos tales que el producto de las distancias desde dos puntos focales es constante (en contraposición a la elipse dónde es la suma a estos la que permanece constante). Concepto En la famosa película de animación Toy Story el vaque...
Leer más

Limite de una funcion en el infinito

Imagen
De manera intuitiva, el límite de una función real en el infinito (o en el menos infinito) es el valor al que se aproxima la función (es decir, su coordenada y) a medida que la coordenada x se hace "más y más grande". En la siguiente imagen queda recogido el concepto y la notación que se suele utilizar: En la imagen, los 4 posibles comportamientos de la función cuando el valor de x crece indefinidamente (decimos, cuando x tiende a ∞). En 1, la función se aproxima a L, por tanto ese es el valor del límite. En 2, la función se va al infinito y en 3 se va a menos infinito. En 4, no existe el límite ya que la función es periódica y no se aproxima a ningún valor concreto. Aproximaciones sucesivas al infinito Ya hemos hablado en apartados anteriores de la estrecha relación que guardan los límites con la idea de aproximarnos sucesivamente a un valor concreto. En este caso, y estrictamente hablando, el infinito no es un valor, sino más bien una idea. ¿Qué significa por tanto que x→∞?...
Leer más